From Theory to Practice: Applying Graph Theory Network Analysis

Graph Theory Network Analysis is a pivotal area within mathematics and computer science that delves into understanding and deciphering the complex networks that encapsulate our world. From the web of social connections to the efficiency of transportation grids, Graph Theory Network Analysis provides the tools and methodologies essential for analyzing and optimizing these networks. This discipline not only enhances our comprehension of theoretical frameworks but also fosters practical applications, making Graph Theory Network Analysis indispensable in both academic research and real-world problem-solving.

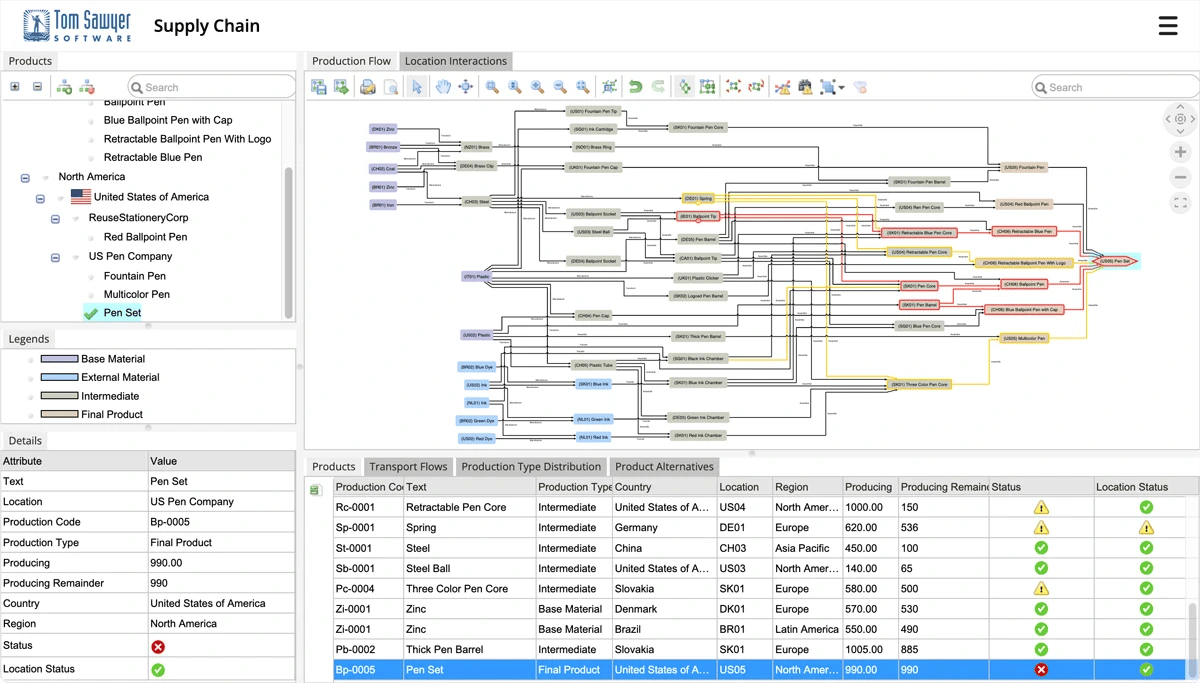
A complex supply chain that applies graph network analysis to highlight at-risk chains.

Introduction to Graph Theory Network Analysis

Graph Theory Network Analysis is a branch of mathematics and computer science that focuses on the study of graphs to model relationships and processes in various systems. It is foundational in understanding the structure and dynamics of networks in diverse fields, including:

• Computer Science: Optimizing algorithms and data structures.
• Biology: Analyzing protein interaction networks.
• Social Network Analysis: Understanding social dynamics and influence patterns.

This interdisciplinary approach not only enhances theoretical knowledge but also propels advancements in practical applications, making it an indispensable tool in today's data-driven world.

Core Principles of Graph Theory

Graph Theory, a fundamental component of network analysis, focuses on the study of graphs as models of interconnected systems. Central to graph theory are nodes (or vertices) and edges (or links), which represent the entities and their connections within a network, respectively. Nodes can symbolize various objects, such as computers in a network, individuals in social networks, or stations in transportation systems, while edges denote the relationships or pathways between them.

Graphs are categorized based on their properties, such as being directed or undirected, and weighted or unweighted. Directed graphs have edges with a specific direction, indicating a one-way relationship, whereas undirected graphs feature bidirectional connections without a specified direction. Weighted graphs assign values or weights to edges, reflecting the strength or capacity of connections, unlike unweighted graphs where all connections are considered equal.

These core principles lay the groundwork for exploring complex networks across different domains, from computer algorithms and biological systems to social structures, highlighting graph theory's versatility and its critical role in dissecting and optimizing networked systems.

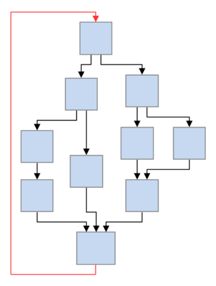
A simple graph showing cycle analysis algorithm applied to find cycles and circular dependencies in a graph.

Key Concepts and Terminologies

In Graph Theory Network Analysis, several foundational terms are pivotal:

• Adjacency Matrices: A square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.
• Path: Refers to a sequence of edges that connects a sequence of vertices, with all edges distinct.
• Cycle: A path that starts and ends at the same vertex without repeating any edges or vertices.
• Degree: The number of edges incident to a vertex. In directed graphs, this splits into in-degree and out-degree.
• Connectivity: Indicates how strongly or weakly the nodes in the graph are connected, encompassing concepts like connected components in undirected graphs and strongly connected components in directed graphs.

Graph Algorithms and Their Applications

Graph algorithms, such as Dijkstra's for finding the shortest path, and Prim's and Kruskal's for identifying minimum spanning trees, play a critical role in network analysis. These algorithms, and many others, are instrumental in solving complex problems efficiently. Dijkstra's algorithm, for instance, is pivotal in routing and navigation systems to find the quickest path. 

Prim's and Kruskal's algorithms are widely used in designing networks like telecommunication systems to ensure minimal wiring costs while maintaining robust connectivity.

Tom Sawyer Perspectives, a low-code graph visualization and analysis application development platform, provides these and many more graph algorithms for understanding which nodes or edges are more important than others. Perspectives provides traversal, clustering, partitioning, path, cycle, centrality, network flow, and tree analysis algorithms, to solve problems in digital transformation, digital engineering, supply chain, logistics, social network analysis, and fraud detection and prevention.

The applications of these graph algorithms are key for gaining value and intelligence from data and underscore their significance in optimizing and solving network flow problems across various fields. 

Graph analysis techniques included with Tom Sawyer Perspectives.

Network Analysis in Action

Graph theory plays a pivotal role in understanding the intricacies of various networks, from the social connections we forge to the vast web of the Internet and the complexities of transportation systems. By applying graph theory in network analysis, we unlock powerful insights into the structure, dynamics, and functionalities of these networks. This section reviews the application of graph theory in analyzing social networks, transportation networks, and the Internet, showcasing its indispensable role in deciphering the connections that shape our world.

Social Network Analysis (SNA)

Social networks represent intricate webs of relationships and interactions among individuals, organizations, or even countries. Through graph theory, each entity is a node, and the relationships between them are edges. This framework allows for the analysis of various network properties, such as degrees of connectivity and centrality measures. For instance, centrality measures can identify influential individuals within a social network. 

These insights are crucial for understanding social dynamics, enhancing communication strategies, and even controlling the spread of information or diseases.

Biological Networks and Their Complexities

Transportation networks, encompassing roads, railways, air routes, and shipping lanes, are vital for the movement of people and goods. Applying graph theory to these networks enables the optimization of routes, the identification of critical connections, and the assessment of network robustness. Algorithms like network flow and others included with Perspectives can find the shortest path between two points, significantly improving logistics and reducing costs. Moreover, analyzing paths using Bridge Detection or Unique Paths helps in pinpointing critical infrastructure that, if disrupted, could significantly impact the network's functionality. This analysis is essential for urban planning, disaster response, and enhancing the efficiency of transportation systems.

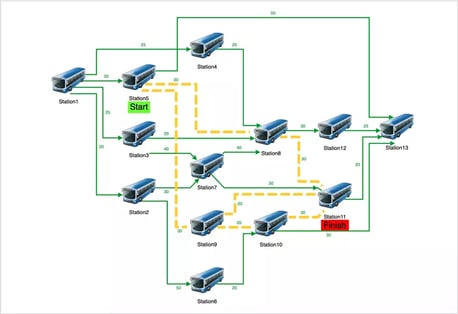
Network flow algorithm applied to find optimal routing of transportation lines.

Tools and Technologies for Graph Theory Network Analysis

Graph theory network analysis has become indispensable across various domains, where the complexity and size of the networks being analyzed necessitate robust tools and technologies. Perspectives is designed specifically for this purpose and, in addition to analysis algorithms, provides robust graph visualization capabilities. 

Visualization plays a crucial role in graph theory network analysis where complex networks, by their nature, are difficult to comprehend through numerical data alone. Visualization provides a way to see the overall structure of the network, identify patterns, and detect outliers or anomalies. Tools like Tom Sawyer Software Perspectives facilitate the exploration of network properties visually, such as community structures, node centrality, and network density. Effective visualization helps in communicating findings to a broader audience, making complex data more accessible and understandable.

Visualization techniques also aid in hypothesis generation and testing by allowing researchers to draw insights from the graphical representation of data. By visualizing the connections and flows within a network, it becomes possible to formulate new theories about the network's behavior and dynamics. This aspect is particularly important in interdisciplinary research, where the graphical representation of networks can bridge the gap between different fields of study.

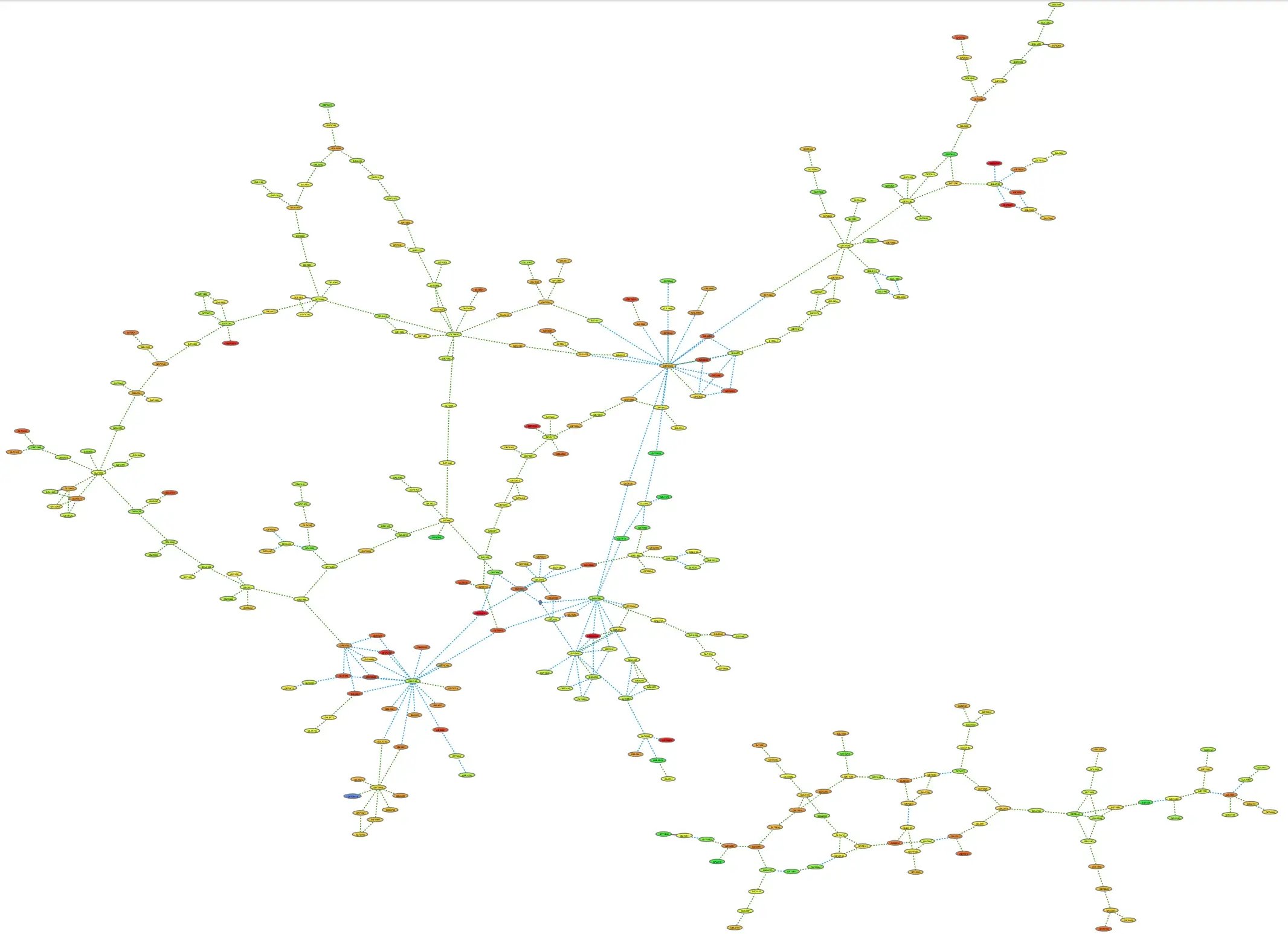
A large graph visualization showing the overall structure of a network produced with Tom Sawyer Software Perspectives.

Challenges and Future Directions

Graph theory network analysis provides insights into the structure and dynamics of complex networks across various domains. However, as networks grow in scale and complexity, the field faces several computational and methodological challenges. Addressing these challenges and exploring future directions is crucial for advancing our understanding and capabilities in network analysis.

Computational Challenges in Large-Scale Networks

Analyzing large-scale networks, such as social networks, transportation systems, or the Internet, presents significant computational challenges. The sheer volume of nodes and edges can lead to exponential increases in the time and memory required for network analysis algorithms. Perspectives provides highly tuned and scalable algorithms that can be used to analyze such large networks.

Additionally, real-world networks often exhibit dynamic behaviors, with nodes and edges appearing or disappearing over time, further complicating the analysis. Developing efficient data structures is essential to overcome these challenges. Parallel computing and distributed systems offer promising solutions by leveraging multiple processors to handle large datasets more effectively.

Integration of AI and Machine Learning

The integration of artificial intelligence (AI) and machine learning (ML) with graph theory and network analysis represents a vibrant future direction. AI and ML can enhance network analysis in several ways, including the prediction of network evolution and identification of patterns or anomalies, for example learning from the structure and behavior of networks to predict future connections. 

Future Trends in Graph Theory and Network Analysis

As we look to the future, several trends are likely to shape the field of graph theory and network analysis:

• Quantum Computing: Quantum computing holds the potential to revolutionize network analysis by performing computations at speeds unattainable by classical computers. This could dramatically reduce the time required for analyzing large-scale networks.
• Network Science as a Service: The rise of cloud computing and as-a-service models may lead to network science being offered as a service. This would make advanced network analysis tools and computational resources accessible to a wider audience, fostering innovation across various sectors.
• Interdisciplinary Approaches: The intersection of network analysis with other disciplines, such as biology, sociology, and physics, is likely to deepen. This interdisciplinary approach can unveil new insights into the fundamental principles governing complex systems.
• Ethical and Privacy Considerations: As network analysis increasingly involves personal data, especially in social networks, ethical and privacy considerations will become paramount. Developing frameworks for ethical network analysis while respecting privacy will be crucial.

Ethical Considerations in Network Analysis

In the realm of network analysis, the increasing ability to collect, analyze, and interpret vast amounts of data from networks—ranging from social media interactions to transportation systems—brings to the forefront ethical considerations. Central among these are concerns related to privacy, security, and the ethical use of network analysis. Addressing these considerations is not only a matter of legal compliance but also one of fostering trust and ensuring the responsible use of technology.

Privacy

Privacy concerns in network analysis primarily revolve around the collection and use of personal data. As networks often contain sensitive information about individuals' behaviors, preferences, and social interactions, it is imperative to safeguard this data against unauthorized access and misuse. Ethical network analysis practices necessitate transparency about data collection methods, adherence to data minimization principles, and obtaining informed consent from individuals whose data is analyzed. Moreover, anonymization and pseudonymization techniques should be employed to protect individuals' identities without compromising the integrity of the analysis.

Security

The security of network data is intrinsically linked to privacy concerns. As network analysis involves storing and processing large datasets, these data repositories become attractive targets for cyberattacks. Ensuring the security of network data involves implementing robust cybersecurity measures, including encryption, access controls, and regular security audits. These measures help prevent data breaches that could expose sensitive information and compromise individuals' privacy.

Ethical Use

The ethical use of network analysis extends beyond privacy and security to include considerations of fairness, accountability, and non-discrimination. Network analysis can potentially reinforce biases present in the data, leading to unfair or discriminatory outcomes. Ethical network analysis requires a conscious effort to identify and mitigate such biases. This involves critically examining the data sources, algorithms, and interpretation of results to ensure that they do not inadvertently harm certain groups or individuals. Furthermore, there should be accountability mechanisms in place to address any adverse outcomes resulting from network analysis.

Conclusion

Graph theory, with its roots deeply embedded in mathematics and computer science, is a cornerstone in the analysis of complex networks across a range of disciplines. Its principles and methodologies provide a powerful lens through which the intricate structures and dynamics of networks can be understood and optimized. By abstracting networks into vertices and edges, graph theory allows for the systematic exploration of relationships, patterns, and anomalies that would otherwise remain hidden in the complexity of raw data.

The significance of graph theory extends beyond academic curiosity, influencing real-world applications ranging from enhancing the robustness of the internet to unraveling human interactions and even advancing medicine through the analysis of biological networks. Its interdisciplinary nature encourages collaboration across fields, fostering innovations that leverage the unique perspectives and techniques of diverse areas of study.

In this data-driven world, further exploration and study in graph theory and network analysis is necessary. The challenges and opportunities presented by large-scale, dynamic networks in an increasingly interconnected world underscore the need for novel approaches, tools, and ethical considerations. By expanding this interdisciplinary field, researchers, practitioners, and enthusiasts can contribute to the development of new knowledge and technologies utilizing networks.

In conclusion, graph theory in network analysis serves as a fundamental tool in deciphering the complexity of interconnected systems, offering insights that drive innovation and understanding across various fields. As the scope of network analysis expands, integrating with emerging technologies and addressing new challenges, network analysis promises to reveal further opportunities. The invitation to explore, innovate, and ethically apply the principles of graph theory in understanding our complex world is promising for those who venture into this interdisciplinary field.

About the Author

Caroline Scharf, VP of Operations at Tom Sawyer Software, has more than 25 years leadership experience at large and small software companies. She has a passion for process and policy in streamlining operations, a solution-oriented approach to problem solving, and is a strong advocate of continuous evaluation and improvement.